Exoplanets

I haven't seen the episode yet but it has often struck me as a remarkably low probability that the orbital plane of an exoplanet would lie exactly in the line of sight between earth and the distant star - and that the exoplanet would conveniently transit the star during the period that said star is observed.

Still, if the sample of stars is big enough - like 100 billion give or take - then perhaps a tiny probability will still throw up a considerable number of candidates...

it has often struck me as a remarkably low probability that the orbital plane of an exoplanet would lie exactly in the line of sight between earth and the distant star

AT LAST!!! An opportunity to put a formula on the forum... my life is complete 🙂

So, the exoplanet transit probability equation...

P ∼ ( R(p) + R(s) ) / a ~ R(s) / a

where R(p) is the planet radius, R(s) is the host-star radius and 'a' is the length of the semimajor axis of the elliptical orbit. We can ignore R(p) providing it is small in comparison to R(s).

So, for example, for the Sun-Earth system, the probability is ~0.005, meaning that we would have to monitor 200 stars to have a chance to detect one transit.

Ye-ess - but that's assuming that the plane of the exoplanet's orbit is in line of sight between the earth and the star. If the plane of the orbit is ever so slightly inclined - or up to 90 degrees relative to line of sight - you can monitor the star all you want but you won't see a transit.

Andy, I follow you and its a great point but wouldn't the probability of the orbital plane be on the same line of sight as our solar system be a bit higher due to the overall flat plane of the galaxy itself? I somehow thought that (rather arrogantly without any scientific enquiring) that most star systems planetary orbital plane would lie in the same plane as the galactic stars orbital plane.

Or are these orbital planes very random from star to star?

Also, for larger exoplanets near the star, line of sight wasn't essential as they used gravitational tugging detection in the early exoplanet finding days (do they still use this technique?).

In terms of differentiating the exoplanet from the star spot, why not combine the transit technique with the gravitational tugging detection and see if there is a correlation? A large planet would at least eliminate a star spot candidate but I guess a small planet would still leave an uncertainty in that the tug is too slight to detect. But can technology feasibly advance to detect the slightest gravitational tug from smaller planets? That would be a next great step to discovering more exoplanets whose orbital planes are not in the line of sight.

Also, our own sunspots don't really hang around for that long do they? Wouldn't it be the same case for other stars? So wouldn't it be a matter of a very short wait time to observe a light dip vanishing hence concluding that "huh, guess that wasn't an exoplanet after all"?

Ouch...what was that? Oh it was Mike's formula, I need to duck quicker next time...

Good points, Tej, and yes I believe you're right about gravitational tugging. And certainly it's my understanding that they do try to deploy as many methodologies as possible to confirm particular exoplanets.

As for the orbital plane, I've been thinking just recently about the path of the Milky Way. As it runs through Cassiopeia, for example, which is a circumpolar constellation at our latitude and therefore quite far north, it seems to me that our solar system's orbital plane is way off compared to the disc of our galaxy. But I've only just started toying with that idea so I have no idea if it stacks up. The different angles at which we see other galaxies also suggests orbital plane randomness, to my mind.

PS: I love your profile, Tej! I read all the way through to the end and wasn't bored at all! 😉

that’s assuming that the plane of the exoplanet’s orbit is in line of sight between the earth and the star

No, it isn't. It only assumes a circular orbit. Eccentric orbits are a little more complex, but the principle is the same.

Have a look at section 2.2 in this paper for a better explanation.

If I've done the maths right, then the penumbra projected by an equivalent sun-earth system is a cone with an angle of around 0.25 degrees - which is about half the angular diameter of the moon. Is that right??? So even allowing for the fact that there is a vastly greater chance that we wouldn't see a transit at all (eg, exoplanet orbital plane perpendicular to our line of sight and all the other angles in between) there is actually a non-trivial likelihood of us being within that cone shadow of shedloads of exoplanet systems. (I'm using 'shedloads' in its astronomical sense - ie, "10 to the power of quite a lot".)

So anyway - while I was thinking about that, I suddenly remembered this cartoon...

While walking home from an awards dinner late last night I suddenly realised that my conclusions above were arrant nonsense. The angular diameter of the conic shadow of an expo planet system bears no relation to the apparent angular diameter as viewed from earth as it clearly depends on the distance of that exoplanet system.

But that paper says "When we are fortunate enough to view an exoplanetary system nearly edge-on, the star and planet periodically eclipse each other" - which I think is pretty much the point I was trying to make: ie, the chances of us actually being able to view an exosystem nearly edge-on must be really quite small. No?

Hi Andy,

Exoplanet transits are really rather common. I think you may be overcomplicating the calculation.

I've just done a quick plot of data on exoplanets.org (an extremely useful resource), which shows the correlation between transit probability and orbital period of the exoplanet:

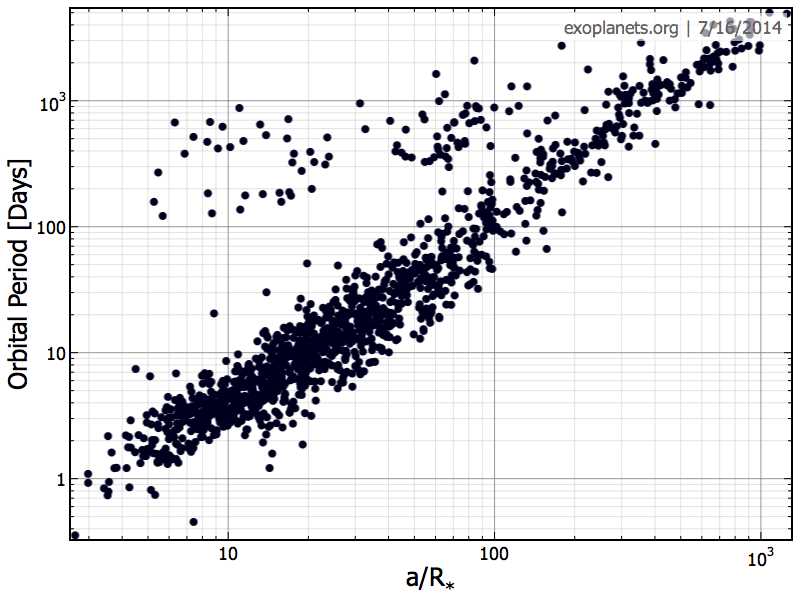
Here, we are seeing a/R(s) rather than R(s)/a, so the lower the number, the higher the probability. As you can see, for exoplanets orbiting close to their parent star (and therefore with a short orbital period), it is really very likely that you will see a transit from Earth. For exoplanets further out (and therefore with a longer orbital period), it is far less likely, but still relatively common when you are looking at thousands of stars.

For example, for the Solar System, the probability of seeing an Earth transit is around 0.5% and a Venus transit is around 0.7%. If one ignores "grazing" transits, which are difficult to view, if other planetary systems are similar to our solar system in that they also contain two Earth-size planets in inner orbits, then approximately 1% of the solar-like stars with planets should show Earth-size transits.

OK Mike, you seem to be more clued up, although Andy's cartoons are admirable!

Andy still has a point about the the line of sight transits, though, I feel.

Looking at your formula, Mike, I really dont see any element of consideration for whether a star system's orbital plane is edge on?

Now just thinking through it logically, step by step, shouldnt the first calculation step be to narrow down the probability of a planetary star system being edge on? Once we have this percentage then we can apply the probability of an exoplanet transit with the formula toys I see you two are having so much fun with.

So question. Can we actually detect the polar axis of a star? Can we detect its rotation direction? If so, assuming all planetary systems orbital planes are perpendicular to the star's axis (I am thinking this is a near 100% certainty, would I be right?), why can't we simply calculate the probability from the existing ratio of stars observed so far divided by the stars whose axis is perpendicular to our line of sight?

Then on those qualified star systems, we can start apply all the factors of an exoplanet transit, which from Mike's formula very logically boils down to the ratio of the elliptic maximum radius of a planet and the Sun's radius.

Also, what would be the time frame for the probability equation to apply? I see no time variables used because the probability of getting a transit in one night is obviously a great deal lower than over a longer time span.

And then we can crank up that probability figure by adding the percentage of exoplanetary systems found via gravitational tug and whose star axis is not perpendicular to our line of sight.

I really dont see any element of consideration for whether a star system’s orbital plane is edge on

Yes, this is taken into account...

See this diagram (with apologies to Nasa, from whom I've nicked it):

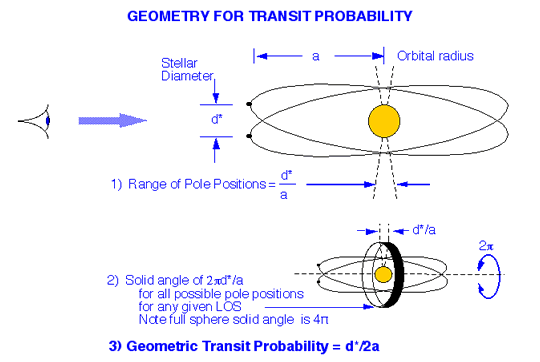
In this case, the formula is shown as d(s) / 2a, which is the same as R(s) / a .

To quote the explanation in full:

"Transits can only be detected if the planetary orbit is near the line-of-sight (LOS) between the observer and the star. This requires that the planet's orbital pole be within an angle of d*/a (part 1 of the diagram) measured from the centre of the star and perpendicular to the LOS, where d* is the stellar diameter (= 0.0093 AU for the Sun) and a is the planet's orbital radius.

This is possible for all 2pi angles about the LOS, i.e., for a total of 4pi d*/2a steradians of pole positions on the celestial sphere (part 2 of the diagram).

Thus the geometric probability for seeing a transit for any random planetary orbit is simply d*/2a (part 3 of the diagram) (Borucki and Summers, 1984, Koch and Borucki, 1996)."

Tej and Andy I have to say I agree with Mike. If you think about it the point is can we observe the planet transit, by what ever method, if so we are then in a position to record data. If we cannot observe the planet then we have no data regarding a transit. The planet has to be in our line of sight.

The planet has to be in our line of sight.

I think we're actually agreeing with each other, Brian!

My original comment was "it has often struck me as a remarkably low probability that the orbital plane of an exoplanet would lie exactly in the line of sight between earth and the distant star". The mathematical formula showing the probability of seeing a transit only work for those small (tiny?) number of exosystems where the orbital plane lies in our line of sight with the star.

The point I was trying to make was mild bemusement at how many exoplanets we are finding given that we have no chance of seeing transits for all the vast numbers other exoplanets whose orbital planes aren't so conveniently positioned. (I haven't yet got my head around Mike's Nasa paper which seems possibly to deal with this.)

So - assuming only that all those episodes that we're recording as exoplanet transits are, in fact, transits and not some other phenomenon, I think there's two conclusions here:
(1) There are potentially vast numbers of exoplanets when you consider all the ones for which we will never even see a transit because their orbital plane isn't cooperating; and
(2) There are potentially quite a lot more exoplanets whose distance from their star and hence their orbital period means that they have not yet had a chance to transit their star (at least, not while we're watching) - the exoplanet Neptunes, so to speak.

Let me try this another way ("God, no! Make him stop!")

Assume every star has an exoplanet, and that that exoplanet whizzes around its star every few months - so there is no excuse for us not seeing them.

But - what proportion of those exoplanets would actually be observable from earth, if the angle of their orbital plane relative to our line of sight is, in fact, random?

EDIT: Hmm. I'm starting to think spherically in terms of all the possible tilts of the angle of the orbital plane - and it's starting to make sense...